Suki Tekverk, a summer intern, spent the last two weeks here studying APL. She will be a high school senior next September and is adept in math, so in addition to APL we also considered some math problems, proofs, and proof techniques, including the following:

Given line segments x and y, construct (using compass and straight-edge) line segments for the following values:
   x+y
   x-y
   x×y
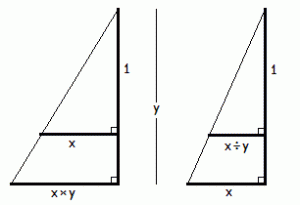
   x÷y

The first two are immediate. Constructing the last two are straightforward if you are also given 1 (or some other reference length from which to construct 1). Can you construct x×y and x÷y without 1?

Constructing x÷y is impossible if you are not given 1 : From x and y alone you can not determine how they compare to 1. If you can construct x÷y, then you can construct x÷x and therefore relate x and y to 1, contradicting the previous statement.

Can you construct x×y without 1? I got stuck (and lazy) and posed the question to the J Chat Forum, and received a solution from Raul Miller in less than half an hour. Miller’s proof recast in terms similar to that for x÷y is as follows:

From x and y alone you can not determine how they compare to 1. If you can construct x×y, then you can construct x×x, whence:
   if x<x×x then x>1
   if x=x×x then x=1
   if x>x×x then x<1
contradicting the previous statement.

I last thought about this problem in my first year of college many decades ago. At the time Norman M. (a classmate) argued that there must be a 1 and then did the construction for x÷y using 1. I recall he said “there must be a 1” in the sense of “1 has to exist if x and y exist” rather than that “you have to use a 1 in the construction” or “you can not construct x÷y without using 1”. I don’t remember what we did with x×y; before Miller’s message I had some doubt that perhaps we were able to construct x×y without using 1 all those years ago. (Norman went on to get a Ph.D. at MIT and other great things.)

Follow