Monthly Archives: April 2017

Displaying cross-references with SharpPlot

Posted on by

Requirements: Update SharpPlot to v3.37 from my.dyalog.com > Downloads > Tools & Interfaces > GUI Tools > SharpPlot

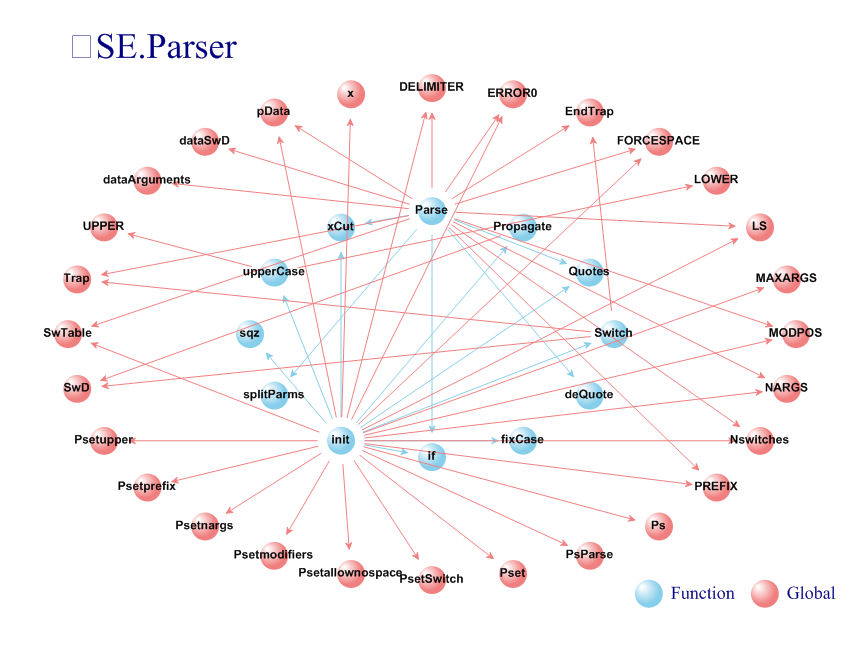
SharpPlot v3.37 introduces Network Maps as a new chart type, and we’re going to use it to display the output of the ]XRef user command, which displays cross-references between all kinds of APL names :

      ]XRef ⎕SE.Parser
             DDEEEFLLMMNNPPPPPPPPPPPQQSSSTUaaaabbbcdddddddfffiilmmmmmmnnnnnnppppqqqqrrrsssssssssstttttuvvvxx∆⍵⍺ 
             EeRnrOOSAOAsRrsssssssss.uwwwrPrrrr:alu.aaaeee.ei.fq.aeioo.adeop.Daa.1mq.et:eipqtwwww:aqwxp.an.C... 
             LlRd:RW.XDRwEo:.eeeeeee.oDTiaPgggg:d.t.tttQff.ax.:..smndd..awv..art..:..qb:t.lzr.imp:b.vtp.lc.u... 
             I.OT:CE.APGiFp:Pttttttt.t.atpE.psv:....aaau.i.tC.:..k.lei..:....tm...:....:..i.:.tao:l...e....t... 
             M.Rr:ER.ROStIa:a........e.bc.R.o.a:....:..o.n.ua.:....elf..:....as...:....:..t.:..ts:e...r....:... 
             I.0a:S..GS.cXg:r.Samnpu.s.lh.:.s.l:....:ASt.e.rs.:....n.i..:....:....:....:..P.:....:....C....:... 
             T..p:P..S:.h.a:s.wloarp.:.e..:...u:....:rwe.d.ee.:....:.e..:....:....:....:..a.:....:....a....:... 
             E...:A...:.e.t:e.ildrep.:....:...e:....:gD..:.s..:....:.r..:....:....:....:..r.:....:....s....:... 
             R...:C...:.s.e:..toigfe.:....:...s:....:u...:....:....:.s..:....:....:....:..m.:....:....e....:... 
             ....:E...:....:..cwfsir.:....:....:....:m...:....:....:....:....:....:....:..s.:....:....:....:... 
             ....:....:....:..hni.x..:....:....:....:e...:....:....:....:....:....:....:....:....:....:....:... 
             ....:....:....:...oe....:....:....:....:n...:....:....:....:....:....:....:....:....:....:....:... 
             ....:....:....:...sr....:....:....:....:t...:....:....:....:....:....:....:....:....:....:....:... 
             ....:....:....:...ps....:....:....:....:s...:....:....:....:....:....:....:....:....:....:....:... 
             ....:....:....:...a:....:....:....:....:....:....:....:....:....:....:....:....:....:....:....:... 
             ....:....:....:...c:....:....:....:....:....:....:....:....:....:....:....:....:....:....:....:... 
             ....:....:....:...e:....:....:....:....:....:....:....:....:....:....:....:....:....:....:....:... 
 [FNS]        - - - - : - - - - : - - - - : - - - - : - - - - : - - - - : - - - - : - - - - : - - - - : - - - - 
 Parse       G.GG○G G GGGG. . . : . ○F.G.G:○○○○○! . ○GGF.○. .○F ○ .○. . ○!○○○G○○! : .○○○○ F :○○○○○○ ○ : ○○.F! . 
 Propagate    ○ . . . : . . . . : . . G . : . .○. . : . . . . : . . .○. : . . . . : . . .○. ○○. . . . :○. . . . 
 Quotes       . . . . : . . . . : . ○ . . : . . . . : . . . .○: .○. . ○ : . . . . ○ . . . . ○ . . .○. : . . . . 
 Switch       . G . . : . . . . : . . G .G: . . . . : . ○ . . : . . . . : . . . . : ○ .○. . : . . . . :○. . . . 
 deQuote      . . . . : . . . . : . . . . : . . . . : . . . . :○○ . . . : . . . . : . . . . ○ . . . . : . . . . 
 fixCase      . . . . : . . . . : . . . . : . . . . : . . . . : . . . . : . . . . : . . . . : . . . . : . . .○. 
 if           . . . . : . . . . : . . . . : . . . . : . . . . : . . . . : . . . . : . . . . : . . . . : . . . . 
 init        G.G. G GGGGGGFGGGGGGGGG.F.GF :○. .○. ○ : . . ○○F F . ○ ○ ○○: . .G. . : . . . .F: . . . . F . GF. . 
 splitParms   . . . . : . . . . : . ○ . . : . . .○.○: . . . . : . . . ○ : .○○ ○ ○○:○. .○. . : . .○. .○: . . . . 
 sqz          . . . . : . . . . : . . . . : . .○. . : . . . . : . . . . : . . . . : . .○. . : . . . . : . . .○. 
 upperCase    . . .G. : . . . . : . . . . G . .○. . : . . . .○: . . . . : . . . . : . .○. . : . . . . : . . .○. 
 xCut         . . . . : . . . . : . . . . : . . . . : . . . . : . . . . : . . . . : . . . . : . . . . : . . .○○

We can capture the output of the user command by doing either
]mat←XRef ⎕SE.Parser (from session)
or
mat←⎕SE.UCMD']XRef ⎕SE.Parser' (from code)

Until Dyalog v16.0 (which has ]XRef -raw), we need to parse the output of ]XRef to get a square link matrix, along with the full list of nodes (in row/column order of the matrix) and list of original rows (functions).

    ∇ (mat nodes rows)←GetMatrix mat;nodelabs;rows;cols;labs;cat;diag
      (rows mat)←2↑(1,2</∧⌿mat=' ')⊂[2]mat        ⍝ cut at empty column
      (cols mat)←2↑(1,2<⌿∧/mat∊' -:')⊂[1]mat      ⍝ cut at - - - - : - - - -
      mat←1↓[1](' '∨.≠mat)/mat                    ⍝ trim first row and empty columns
      rows←~∘' '¨↓(-1⊃⍴mat)↑[1]rows               ⍝ row titles (list of strings)
      cols←~∘' .:'¨↓(-2⊃⍴mat)↑[1]⍉cols            ⍝ col titles (list of strings)
      nodes←rows∪cols                             ⍝ all titles
      mat←((mat,' ')⍪' ')[rows⍳nodes;cols⍳nodes]  ⍝ square matrix of nodes
    ∇

Now let’s wrap the SharpPlot initialisation into a single function that uses the .NET version if available and falls back to the cross-platform APL workspace if not:

    ∇ {dotnet}←Init
      :If dotnet←(,'W')≡3⊃'.'⎕WG'APLVersion'
          ⍝ .Net assembly (windows only)
          ⎕USING←',sharpplot.dll' ',system.drawing.dll'
      :Else
          ⍝ APL workspace (all platforms)
          :If 0=⎕NC'Causeway'   ⍝ copy workspace only once
              (System.Drawing←System←⍎'Causeway'⎕NS'').(⎕CY'sharpplot.dws')
          :EndIf 
      :EndIf
    ∇

Then we can write a platform-independent function that returns the SharpPlot instance with the chart drawn on it. We split nodes into two categories, functions and globals (ignoring locals and labels) and split links by destination node. By default, DrawNetworkMap lays out node categories on co-centric circles. Also, because the graph is uni-directional, we can afford to use straight links without damaging readability:

    ∇ sp←name Plot(mat nodes rows);catlabs;nodecat
      sp←⎕NEW Causeway.SharpPlot
     
      catlabs←'Function' 'Global'    ⍝ links are split by destination node
      nodecat←(≢nodes)⍴0             ⍝ ignored by default
      ((∨⌿mat∊'FR*')/nodecat)←1      ⍝ functions
      ((∨⌿mat∊'G')/nodecat)←2        ⍝ globals
      ((nodes∊rows)/nodecat)←1       ⍝ caller functions
     
      sp.Heading←name
      sp.HeadingStyle←Causeway.HeadingStyles.Left
      sp.SetMargins 40 30 30 30
      sp.KeyStyle←Causeway.KeyStyles.(BottomAlign+RightAlign)
      sp.SetILabels⊂nodes
      sp.SetILabelFont'Arial' 6 System.Drawing.FontStyle.Bold System.Drawing.Color.Black
      sp.SetColors⊂System.Drawing.Color.(SkyBlue LightCoral)
      sp.SetMarkers Causeway.Marker.Ball
      sp.SetMarkerScales 2
      sp.SetLineStyles Causeway.LineStyle.Solid
      sp.SetPenWidths 0.5
      sp.NetworkMapStyle←Causeway.NetworkMapStyles.(SplitByDestination+Dissected+ArrowLines+FixedArcs+NoAxes+NoLinkKey)
      sp.SetNetworkMapLinkArc 0         ⍝ straight lines
      sp.SetArrowStyle 5                ⍝ fixed-size arrows
     
      sp.SplitBy nodecat catlabs
      sp.DrawNetworkMap⊂↓(mat∊'GFR*')   ⍝ use a single width for all valid links
    ∇

We can then save the graph as SVG to a file (here we use the SvgMode that scales the SVG to fit its container):
sp.SaveSvg 'XRef.svg' Causeway.SvgMode.FixedAspect

Or, if feeding a web server or renderer, we can grab the SVG as a single string without writing to disk:
svg←sp.RenderSvg Causeway.SvgMode.FixedAspect

Windows users will be able to use the SharpPlot Viewer:
vw←⎕NEW Causeway.SharpPlotViewer sp
vw.Show ⍬

XRef

More examples of Network Maps can be found on the SharpPlot.com website in the Network Map Tutorials. To translate C# examples into APL, you can refer to the SharpPlot Rosetta Stone.

Email, RSS Follow

Calculation v Look-Up

Posted on by

(⎕io←0 and timings are done in Dyalog version 15.0.)

Table Look-Up

Some functions can be computed faster by table look-up than a more traditional and more conventional calculation. For example:

      b←?1e6⍴2

      cmpx '*b' '(*0 1)[b]'
 *b        → 1.32E¯2 |   0% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕
 (*0 1)[b] → 1.23E¯3 | -91% ⎕⎕⎕

Some observations about this benchmark:

(a) The advantage of table look-up depends on the time to calculate the function directly, versus the time to do indexing, ⍺[⍵] or ⍵⌷⍺, plus a small amount of time to calculate the function on a (much) smaller representative set.

Indexing is particularly efficient when the indices are boolean:

      bb←b,1
      bi←b,2
      cmpx '2 3[bb]' '2 3 3[bi]'
 2 3[bb]   → 1.12E¯4 |    0% ⎕⎕⎕⎕⎕
 2 3 3[bi] → 7.39E¯4 | +558% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕

bi is the same as bb except that the last element of 2 forces it to be 1-byte integers (for bi) instead of 1-bit booleans (for bb).

(b) Although the faster expression works best with 0-origin, the timing for 1-origin is similar.

      cmpx '*b' '{⎕io←0 ⋄ (*0 1)[⍵]}b'
 *b                   → 1.32E¯2 |   0% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕
 {⎕io←0 ⋄ (*0 1)[⍵]}b → 1.22E¯3 | -91% ⎕⎕⎕

That is, if the current value of ⎕io is 1, the implementation can use a local ⎕io setting of 0.

(c) The fact that *b is currently slower than (*0 1)[b] represents a judgment by the implementers that *b is not a sufficiently common computation to warrant writing faster code for it. Other similar functions already embody the table look-up technique:

      cmpx '⍕b' '¯1↓,(2 2⍴''0 1 '')[b;]'
 ⍕b                   → 6.95E¯4 |  0% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕
 ¯1↓,(2 2⍴'0 1 ')[b;] → 6.92E¯4 | -1% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕

Small Domains

Table look-up works best for booleans, but it also works for other small domains such as 1-byte integers:

      i1←?1e6⍴128    ⍝ 1-byte integers

      cmpx '*i1' '(*⍳128)[i1]'
 *i1         → 1.48E¯2 |   0% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕
 (*⍳128)[i1] → 9.30E¯4 | -94% ⎕⎕

      cmpx '○i1' '(○⍳128)[i1]'
 ○i1         → 2.78E¯3 |   0% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕
 (○⍳128)[i1] → 9.25E¯4 | -67% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕

In general, a table for 1-byte integers needs to have values for ¯128+⍳256. Here ⍳128 is used to simulate that in C indexing can be done on 1-byte indices without extra computation on the indices. In APL, general 1-byte indices are used as table[i1+128]; in C, the expression is (table+offset)[i].

Domains considered “small” get bigger all the time as machines come equipped with ever larger memories.

Larger Domains

Table look-up is applicable when the argument is not a substantial subset of a large domain and there is a fast way to detect that it is not.

      i4s←1e7+?1e6⍴1e5    ⍝ small-range 4-byte integers

      G←{(⊂u⍳⍵)⌷⍺⍺ u←∪⍵}

      cmpx '⍟i4s' '⍟G i4s'
 ⍟i4s   → 1.44E¯2 |   0% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕
 ⍟G i4s → 9.59E¯3 | -34% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕

The definition of G implements that the argument is not used directly as indices (as in (⊂⍵)⌷⍺⍺ u) but needed to be looked up, the u⍳⍵ in (⊂u⍳⍵)⌷⍺⍺ u. Thus both index-of and indexing are key enablers for making table look-up competitive.

§4.3 of Notation as a Tool of Thought presents a different way to distribute the results of a calculation on the “nub” (unique items). But it takes more time and space and is limited to numeric scalar results.

      H←{(⍺⍺ u)+.×(u←∪⍵)∘.=⍵}

      i4a←1e7+?1e4⍴1e3    ⍝ small-range 4-byte integers

      cmpx '⍟i4a' '⍟G i4a' '⍟H i4a'
 ⍟i4a   → 1.56E¯4 |       0%
 ⍟G i4a → 6.25E¯5 |     -60%
 ⍟H i4a → 1.78E¯1 | +113500% ⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕⎕

The benchmark is done on the smaller i4a as a benchmark on i4s founders on the ≢∪⍵ by ≢⍵ boolean matrix (for i4s, 12.5 GB = ×/ 0.125 1e5 1e6) created by H.

Mathematical Background

“New Math” teaches that a function is a set of ordered pairs whose first items are unique:

*⍵: {(⍵,*⍵)|⍵∊C}      The set of all (⍵,*⍵) where ⍵ is a complex number
⍟⍵: {(⍵,⍟⍵)|⍵∊C~{0}}  The set of all (⍵,⍟⍵) where ⍵ is a non-zero complex number
○⍵: {(⍵,○⍵)|⍵∊C}      The set of all (⍵,○⍵) where ⍵ is a complex number
⍕⍵: {(⍵,⍕⍵)|0=⍴⍴⍵}    The set of all (⍵,⍕⍵) where ⍵ is a scalar

When ⍵ is restricted (for example) to the boolean domain, the functions, the sets of ordered pairs, are more simply represented by enumerating all the possibilities:

*⍵: {(0,1), (1,2.71828)}
⍟⍵: {(0,Err), (1,0)}
○⍵: {(0,0), (1,3.14159)}
⍕⍵: {(0,'0'), (1,'1')}

Realized and Potential Performance Improvements

realized (available no later than 15.0)

boolean
1-byte integer		 ⍕ ∘.f
⍕     a∘⍕

potential (non-exhaustive list)

boolean
1-byte integer
2-byte integer
small-range 4-byte integer		 * ⍟ | - ○   ! ⍳ a∘f f.g
* ⍟ | - ○ × ! ⍳ a∘f f.g ∘.f
* ⍟ | - ○ ×   ⍳ a∘f
* ⍟ |     ×

a is a scalar; f and g are primitive scalar dyadic functions.

Email, RSS Follow

Supporting the Community – Update

Posted on by

You may have been wondering what has been happening with Jo Shaw (daughter of our Customer Account Manager, Karen) the England pool player who Dyalog have sponsored in the past, so we thought it was time for an update.

After getting a new job in December 2014, Jo moved from Hampshire to Wiltshire and joined the Wiltshire Ladies county pool team. After a successful first season with them, Jo again qualified to play for England as a reserve player in May 2016 but the exciting news that she was expecting a baby meant that she was not able to take up her place in the team – unfortunately the Nation’s Cup event was happening at the exact same time the baby was due. Jo also found that she was not able to practice or play pool during the later stages of her pregnancy as she was just not able to bend over the table(!) so this meant she had to take a back seat with the Wiltshire Ladies county team too.

Jo’s daughter Remy was born on 18 October 2016 and Remy has been a keen supporter of Wiltshire Ladies since she was born – she even has her own team shirt!

Jo and Remy have recently been to the EBPF National Finals to support Jo’s Wiltshire teammates as they became National Ladies Champions for the first time. Jo was disappointed that she wasn’t able to play a bigger part in the victory but being a mother is now her top priority and she was pleased that her team did so well.

After a lot of thought Jo has now made the very difficult decision to take some time out from both county and national pool to concentrate on being a mum. She plans to be back in a year or so once Remy is a bit older and Dyalog fully expect her to win back her place in the England team – we will be there to support her when she does!

Email, RSS Follow