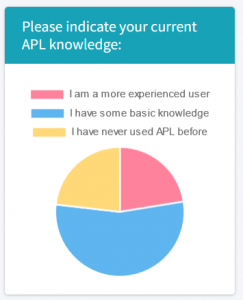
 Last Wednesday we hosted APL Seeds ’23, the third of our free online user meetings aimed at new and prospective users of APL. In attendance was a mix of new users and the APL-curious, as well as more experienced APLers answering questions and imparting wisdom in the chat and during the post-event meetup.
Last Wednesday we hosted APL Seeds ’23, the third of our free online user meetings aimed at new and prospective users of APL. In attendance was a mix of new users and the APL-curious, as well as more experienced APLers answering questions and imparting wisdom in the chat and during the post-event meetup.
Rich Park began the meeting with an introduction to the basic syntax of the language and a sample solution to a problem from last year’s APL Problem Solving Competition – from data about the schedule of an online event, and the times people joined the event, which sessions did each user attend? He demonstrated how the thought process of a solution could map neatly onto an executable APL expression. In particular, he showed how an elegant solution tends towards using primitives directly with array argument values, as opposed to abstracting the solution for one piece and explicitly looping over the collection.
Adám Brudzewsky then explored how to remember unfamiliar ideas. He presented some mnemonic devices linking the glyphs that make up the core APL language with both the concepts that they represent and their locations on the APL keyboard. Whether they are two related concepts represented by the same symbol, or if the dyadic form is the same as monadic with a default left argument, or if two unrelated functions use the same glyph, these tricks are really useful for memorising the fundamental building blocks of APL.

A still screenshot doesn’t do justice to the wonderful animations in Adám’s presentation.
We then heard about learning APL from the perspective of a non-programmer. Richard Savenije is a project director for infrastructure projects in a construction company. After a stint of programming in C at IBM, Richard decided he did not want to pursue programming any further. When he left, he took an APL manual with him, as he had been intrigued by the glyphs. It sat untouched for 28 years, until he recently decided to start learning to solve problems with APL. He told us about the new perspectives he has gained while using APL, and parallels with the type of problem solving he does in his day-to-day life.
APL media often shows the symbols, interesting approaches to algorithms, and other ways in which APL is fascinatingly unique in the world of programming languages. However, this often leaves people wondering whether they could use this in the more pedestrian tasks of automation, data processing, and application development. The final two talks of the day addressed the more practical use of APL.
You might have heard Stefan Kruger’s name before – he wrote the excellent Learning APL book and gave a presentation at APL Seeds ’22. He acknowledged that the domain of APL is largely seen as “super tight” numerical algorithms and array transformations. This year he explained the convenience of HttpCommand and ⎕JSON for ingesting data from external sources, and explored the creation of user commands to provide a convenient interface for performing repetitive tasks. Stefan used these to rewrite a substantial collection of (mostly Python) utility scripts as APL functions and user commands, ultimately shrinking the code by a factor of 10!
Stefan shows us how to construct user commands to conveniently perform repetitive tasks.
In the final presentation of the day, Josh David answered the question of “what does it look like when my APL Seeds come to fruition?” He began with a demonstration of some analysis of water potability data that turned out to look dangerous – or fake. Throughout his demonstration, we got a feeling for how to rapidly inspect and transform data to gain insights. He included plenty of very useful tips for new APLers, such as how to stop the stream of text into the session when you execute an expression that produces long output (Action > Interrupt in the Session menu…there are more tips like this on our website). Finally, he showed some full-stack graphical applications – his SQL-Browser and The Carlisle Group’s FlipDB – with examples of database connectivity, querying and analysis.
After the talks, there was an informal online meetup. This included lively discussion about many topics, including language design and terminology. We also discussed questions about teaching tacit programming, and heard perspectives from some APL beginners – if someone is learning the concept of functions for the first time, then composition of functions is probably not appropriate at that point.
We hope we were able to spark interest, give some clarity to people’s image of APL, and inspire you to start or continue learning and using APL. Relevant materials have been uploaded to the APL Seeds ’23 webpage, including links to recordings of the presentations on dyalog.tv.
 Jada first heard about APL when her partner, Rich Park, joined Dyalog Ltd in October 2018. Since then, she has attended various Dyalog Ltd events as a guest, including Dyalog ’19 and Dyalog ’22, and found the enthusiasm and passion of the APL community infectious, despite having little to no experience in computing. Attending these events left Jada with a very positive impression of Dyalog Ltd, particularly with the logistical planning and administrative organization evident from the smooth running of each event. She was also in the unique position of being able to interact with Dyalog Ltd employees prior to joining the company, fostering good relationships through casual communication.
Jada first heard about APL when her partner, Rich Park, joined Dyalog Ltd in October 2018. Since then, she has attended various Dyalog Ltd events as a guest, including Dyalog ’19 and Dyalog ’22, and found the enthusiasm and passion of the APL community infectious, despite having little to no experience in computing. Attending these events left Jada with a very positive impression of Dyalog Ltd, particularly with the logistical planning and administrative organization evident from the smooth running of each event. She was also in the unique position of being able to interact with Dyalog Ltd employees prior to joining the company, fostering good relationships through casual communication.


 Follow
Follow Last Wednesday we hosted
Last Wednesday we hosted 



 When not programmaing, Silas can be found enjoying a good book and the occasional summer hike with friends and family.
When not programmaing, Silas can be found enjoying a good book and the occasional summer hike with friends and family.









