Each week until early January, we will be releasing a selection of recordings of presentations from Dyalog’18, which was held in Belfast at the end of October 2018. Last week we kicked off with the opening keynote talks and the prize ceremony and acceptance speech by the winner of our annual problem-solving competition.
Just under half of the presentations at Dyalog User Meetings are by users who have volunteered – or sometimes been commandeered – to share stories about how they have used APL for fun or profit. These user stories provide significant motivation to the Dyalog team for future direction.
Aaron Hsu’s talk on “High Performance Tree Wrangling, the APL Way” is a pearl. Back in 2015 I gave a talk at Google on APL. One of the Google engineers asked about working with trees in APL and I was unable to give him a useful answer. Aaron is working on a compiler for APL, and trees that represent the code that is being compiled are his most important type of data structure.
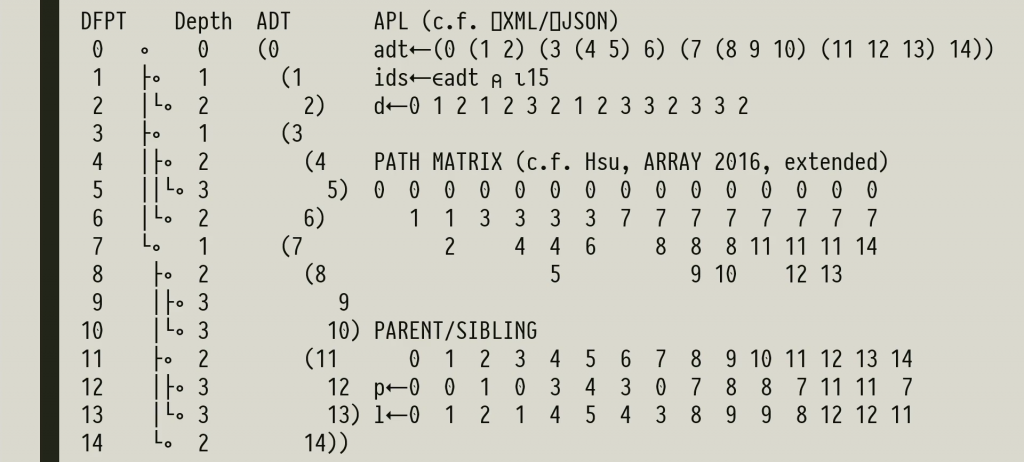
In this talk Aaron demonstrates that APL is an elegant – and highly efficient – notation for working with trees, if you just pick the right representation!

Most of the talks at Dyalog User Meetings are fairly technical. The subject at the core of Ilaria Piccirilli’s talk – the fair pricing of financial instruments and subsequent evaluation of portfolios – is no exception. Mercifully, Ilaria spares us the details of the calculations – as she dryly notes, there is no “Fair Pricing for Dummies”. Instead, she offers humorous insights into the way her team used APL to deal with the explosion of computations required by regular additions to legislation requiring health checks – and the day that negative interest pulled the rug out from under most standard pricing calculations.
The other, slightly larger half of the talks at Dyalog Users meetings are by members of the Dyalog Team, talking about work that has recently been done on our products or presenting designs for future enhancements.

Adám Brudzewsky’s talk, titled Array Notation Mk III, is about a potential future extension to the APL language, which will make it possible to easily and clearly describe arrays of high rank, or with deeply nested structure, without using APL primitives to “construct” them, as is common practice today. In addition to making application code easier to read and write, a literal notation for data structures will make it easy to use text files to describe data structures which are essentially part of the source code of an application, and should be managed by a source code management system. As the name suggests, this work has been ongoing for some time, with the initial inspiration coming from a user presentation by Phil Last, back at Dyalog ’15 in Sicily. Watch the presentation and give us feedback on whether you think this idea is now sufficiently baked to become part of Dyalog APL, or we’ll need a “Mk IV” talk next year!

With the growth in usage of Dyalog APL under macOS and Linux – especially in server or cloud environments – the Dyalog Remote Integrated Development Environment is becoming a “mainstream” tool, rather than the curiosity that it was during the first few years of development. Our partners at Optima Systems are developing RIDE on Dyalog’s behalf, and Gilgamesh Athoraya is now the lead developer. In his talk on “RIDE 4.1 and Next Generation Integrations”, Gil talks first about significant new features and performance improvements to RIDE in 4.1 – and then continues to talk about how components of the RIDE technology may be re-purposed to provide APL add-ins for popular development frameworks like the new Microsoft VS Code.
Summary of this week’s videos:


 Follow
Follow