Today we reach two very significant milestones.
40 Years of Dyalog APL
On this day, we have cause for celebration: it is 40 years since the release of Dyalog version 1.0! Geoff Streeter would say that from his perspective we are already in the 42nd year, as he and John Scholes started work on the new interpreter in 1981. On the other hand, Pete Donnelly might argue that the interpreter wasn’t really ready for serious use until a few years after that date. The fact remains that the APL ’83 conference in Washington DC saw the first official release of the product, and is considered to be the “birth” of Dyalog APL.



Farewell Geoff Streeter
On the same day, we also congratulate Geoff Streeter, the last Dyalog developer who will have worked on the interpreter throughout its existence, on the first day of his retirement. We are happy to be able to report that, unlike John Scholes who designed and built version 1.0 together with Geoff but sadly passed away in 2019, Geoff is retiring in good health. We wish him many happy years in retirement in the company of his wife Sarah, children and grandchildren – although we are also hoping that he will pop by the Dyalog office from time to time to let us know how he thinks we are doing, and hopefully also join us at some future user meetings!
Continuity
It is impossible to exaggerate the value of the dedication and continuity that Geoff and John provided to Dyalog over these four decades. In the early days, when company finances were shaky, they sometimes continued work on the interpreter without compensation. Today, we are still blessed with many team members who have worked for Dyalog for most, if not all, of their careers – although we are doing what we can to avoid the need for the extremes of dedication that were required in the early days.
Good Choices
Dyalog APL started its life as a unique combination of what was to become the leading nested array paradigm (APL2/NARS floating arrays) coupled with what John and Geoff (and the rest of the consulting team at Dyadic Systems Ltd) thought were the best “commercial” extensions selected from APL systems developed by STSC and I.P.Sharp Associates (component files and control structures from STSC, error trapping from IPSA, and many other features).
The early choices have stood the test of time, and paved the way for Dyalog to become extremely competitive when Windows 3.1 and John Daintree arrived at the same time – resulting in the extremely easy-to-use Win32 GUI support. In typical fashion, the team did not merely implement a tool for GUI programming, they adopted an approach that led to the very general notion of namespaces, which meant that the same architecture could be used to interface to COM/OLE and subsequently .NET and complete support for object-oriented programming in Dyalog.
UNIX
Geoff was (and is) very much a UNIX man, and the first versions of Dyalog were built for the small UNIX machines that Dyadic Systems expected to take over from the mainframe. Unfortunately, UNIX was slow to gain acceptance and, around 1990 when UNIX was finally starting to take off, Microsoft Windows arrived and the centre of gravity of the commercial business shifted in that direction. Geoff was often heard muttering to himself about how the company was making poor technical choices, driven by what he referred to as “commercial” pressure. He kept his head down, and ensured the UNIX implementations were well supported and that all designs took the needs of these platforms into account.
Users of UNIX-based Dyalog can be grateful for Geoff’s unwavering enthusiasm. And Dyalog too: not only is the IBM AIX version of APL still a significant source of revenue, the ease with which we have been able to add support for Linux and macOS is very much down to our long UNIX history and the goal of maintaining cross-platform compatibility, throughout the history of the product.
Dedication
As a further example of Geoff’s dedication: as a young man with a motorcycle and a keen sense of community, Geoff started riding at night, delivering blood from blood banks to hospitals where it was urgently needed. He started doing this in 1980, just after he started at Dyadic Systems, and, although he is retiring from Dyalog today, Geoff will continue as a volunteer for SERV S&L. Although he no longer rides his bike, he now acts as the controller for the new generation of riders. In October 2021, SERV S&L was presented with The Queen’s Award for Voluntary Service by the Lord Lieutenant of Surrey.

The Future
In the same way that Geoff has not been riding his bike at night, he has not been doing any new development on Dyalog for the last year. Instead, he has been preparing and holding internal presentations to a new generation of Dyalog developers, providing insight into the work that he has done over the last four decades. Ultimately an impossible task of course, but at least they now know where to start digging – and Geoff is still around to answer questions in an emergency if we offer him a cup of coffee and three plain chocolate digestives (his stated minimum requirement to come into the office!).
As Dyalog enters its fifth decade, all parts of Dyalog Ltd. (including the development team) are larger – and broader – than they have ever been. The good choices made by Geoff, John, Pete, and many others in the early years are holding up, and the company continues to grow.
Many thanks to Geoff from everyone at Dyalog Ltd. We will do our best to allow him to relax, enjoy his well-deserved retirement, and look forward to continued dividend payments from the Dyalog shares in his pension fund!
References:


 Follow
Follow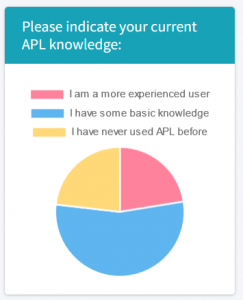 Last Wednesday we hosted
Last Wednesday we hosted 


 When not programmaing, Silas can be found enjoying a good book and the occasional summer hike with friends and family.
When not programmaing, Silas can be found enjoying a good book and the occasional summer hike with friends and family.