This gallery contains 2 photos.
Last night’s whisky and chocolate tasting Last night’s dinner ended with a talk from Glengoyne, a highland distillery based fourteen miles north of Glasgow. We were presented with three different whiskies in their range, and a talk explaining how they were produced … Continue reading
#Dyalog’16 – Vibeke Ulmann Today we had the first of the 3 grand prize winner presentations. Joshua David is 19 years old and is in his second year studying Computer Science at the University of Scranton. He is also taking … Continue reading
#Dyalog16 – Vibeke Ulmann As announced earlier – and iterated many times by yours truly, to media and other interested parties, because it is SOOOOOOO exciting – this year, the Viking Challenge is to drive a speed boat in the … Continue reading
This gallery contains 9 photos.
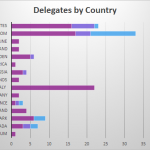
This year at the user meeting we have 106 attendees and a further 15 partners and guests, from 15 different countries worldwide. Today was the first day of presentations and the day the user meeting opened formally. Today also saw the arrival of the … Continue reading
This gallery contains 10 photos.
It was a gloriously sunny day in Glasgow today. The Golden Jubilee Hotel overlooks the River Clyde and this was the view at sunrise: The day began with delegate registration, with Karen and Fiona manning the registration desk throughout the … Continue reading
This gallery contains 4 photos.
Welcome to Glasgow and to Dyalog ’16 – this year’s annual Dyalog user meeting, which is taking place at the Golden Jubilee Hotel on the banks of the River Clyde. Whether you are attending in Glasgow or following from afar, … Continue reading
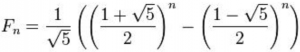
Follow